由leetcode上一道题引发对解空间树的思考
#题目:
Given a non-empty array containing only positive integers, find if the array can be
partitioned into two subsets such that the sum of elements in both subsets is equal.
NOTE:
Each of the array element will not exceed 100.
The array size will not exceed 200.
##Example:
Input: [1, 5, 11, 5]
Output: true
Explanation: The array can be partitioned as [1, 5, 5] and [11].##Example 2:
Input: [1, 2, 3, 5]
Output: false
Explanation: The array cannot be partitioned into equal sum subsets.#思路
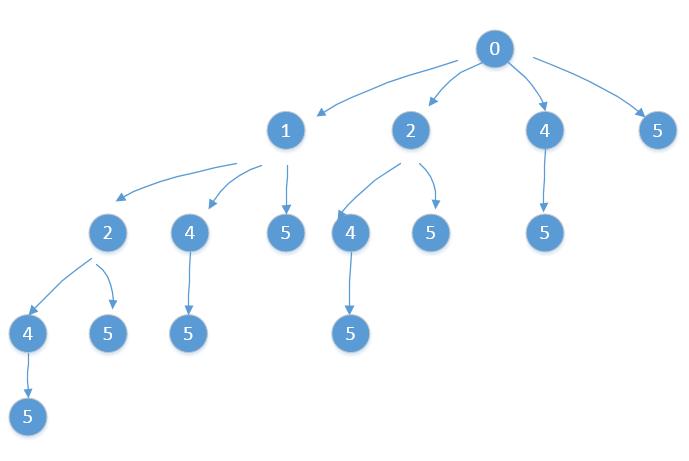
举例 1 4 5 2 output: true
对于排好序的解空间树,如图所示,一开始的根节点设为0
class Solution {
public boolean canPartition(int[] nums) {
//先对nums中的数求和
Arrays.sort(nums); //对数组排序
int sum = 0;
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
}
if(sum%2==1){ //当sum为奇数 则为false
return false;
}
else{ //偶数 能否从nums[] 中 刚好找到一组数的和 = sum/2 若能 则返回true 否则 返回false
sum= sum/2;
//采用DFS暴力解决问题
return dfs(0,sum,nums);
}
}
// 一一尝试
public boolean dfs(int index,int sum,int[] nums){
sum -= nums[index] ;
if(sum == 0) return true;
for(int i=index+1;i<nums.length;i++){
if(sum<nums[i]) break; //排序后,可以剪枝
if(dfs(i,sum,nums)) return true;
}
return false;
}
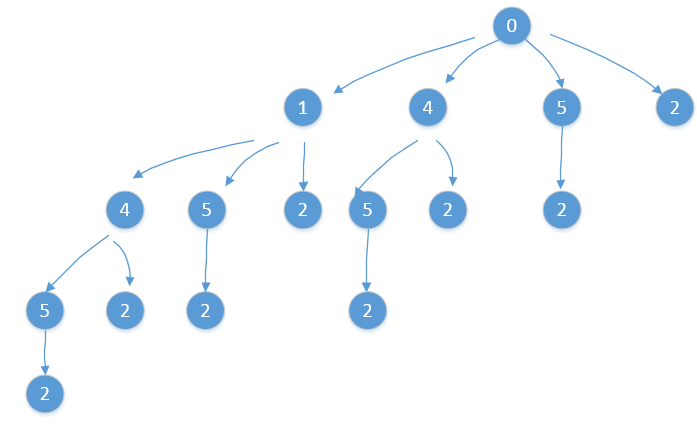
}对于未排好序的解空间树,如图所示,一开始的根节点设为0,不可以剪枝,这些情况都得遍历
class Solution {
public boolean canPartition(int[] nums) {
//先对nums中的数求和
int sum = 0;
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
}
if(sum%2==1){ //当sum为奇数 则为false
return false;
}
else{ //偶数 能否从nums[] 中 刚好找到一组数的和 = sum/2 若能 则返回true 否则 返回false
sum= sum/2;
//采用DFS暴力解决问题
return dfs(0,sum,nums);
}
}
// 一一尝试
public boolean dfs(int index,int sum,int[] nums){
sum -= nums[index] ;
if(sum == 0) return true;
for(int i=index+1;i<nums.length;i++){
if(dfs(i,sum,nums)) return true;
}
return false;
}
}