leetcode上一道很经典的问题
#题目:
Given a set of distinct integers, nums, return all possible subsets.
Note: The solution set must not contain duplicate subsets.
For example,
If nums = [1,2,3], a solution is:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]先介绍两种非递归的写法
#method 1
从上面的二叉树可以观察到,当前层的集合 = 上一层的集合 + 上一层的集合加入当前层处理的元素得到的所有集合(其中树根是空集),因此可以从第二层开始(第一层是空集合)迭代地求最后一层的所有集合(即叶子节点)
/*****************************************************
* 非递归方式求子集 举例 123 [] [1] [2] [1 2] [3] [1 3] [2 3] [1 2 3]
* 1:list [] lists []
* 2.list [1] lists [] [1]
* 3.list [2] [1 2] lists [] [1] [2] [1 2]
* 4.list [3] [1 3] [2 3] [1 2 3] lists [] [1] [2] [1 2] [3] [1 3] [2 3] [1 2 3]
*/
public List<List<Integer>> subsets(int[] nums) {
Arrays.sort(nums);
List<Integer> list = new ArrayList<Integer>();
List<List<Integer>> lists = new ArrayList<List<Integer>>();
lists.add(list);
for (int i = 0; i < nums.length; i++) {
int lists_size = lists.size();
for (int j = 0; j < lists_size; j++) {
List<Integer> l = new ArrayList<Integer>(lists.get(j));
l.add(nums[i]);
lists.add(l);
}
}
return lists;
}
#method 2
由于S[0: n-1]组成的每一个subset,
可以看成是对是否包含S[i]的取舍。
S[i]只有两种状态,包含在特定subset内,或不包含。
所以subset的数量总共有2^n个。所以可以用0~2^n-1的二进制来表示一个subset。
二进制中每个0/1表示该位置的S[i]是否包括在当前subset中。
/****************************************************************
* 由于S[0: n-1]组成的每一个subset,
* 可以看成是对是否包含S[i]的取舍。
* S[i]只有两种状态,包含在特定subset内,或不包含。
* 所以subset的数量总共有2^n个。所以可以用0~2^n-1的二进制来表示一个subset。
* 二进制中每个0/1表示该位置的S[i]是否包括在当前subset中。
*/
public List<List<Integer>> subsetsByBitManipulation(int[] nums) {
List<List<Integer>> lists = new ArrayList<List<Integer>>();
List<Integer> list;
int n = 1<<nums.length;
for (int i = 0; i < n; i++) {
list = num2subset(i, nums);
lists.add(list);
}
return lists;
}
private List<Integer> num2subset(int num,int[] nums){
List<Integer> list = new ArrayList<Integer>();
for (int i = 0; i < nums.length; i++) {
if((num&1) == 1){
list.add(nums[i]);
}
num>>=1;
}
return list;
}接下来采用两种递归的方式来遍历数组
#method 3
采用dfs递归的方式 与二叉树的遍历很像
求集合的所有子集问题。题目要求子集中元素非递减序排列,因此我们先要对原来的集合进行排序。原集合中每一个元素在子集中有两种状态:要么存在、要么不存在。这样构造子集的过程中每个元素就有两种选择方法:选择、不选择,因此可以构造一颗二叉树,例如对于例子中给的集合[1,2,3],构造的二叉树如下(左子树表示选择该层处理的元素,右子树不选择),最后得到的叶子节点就是子集
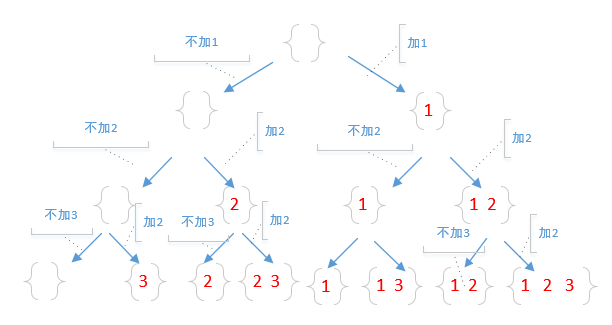 ;
;
/**********************************************************************
* 采用DFS递归的方式求子集
*原数组中每一个元素在子集中有两种状态:
*要么存在、要么不存在。
*这样构造子集的过程中每个元素就有两种选择方法:选择、不选择,
*因此可以构造一颗二叉树来表示所有的选择状态:
*二叉树中的第i+1层第0层无节点表示子集中加入或不加入第i个元素,
*左子树表示加入,右子树表示不加入。所有叶节点即为所求子集。
*因此可以采用DFS的递归思想求得所有叶节点。
*
*和二叉树的遍历很像
*/
public List<List<Integer>> subsetsByDFS(int[] nums) {
List<List<Integer>> lists = new ArrayList<List<Integer>>();
List<Integer> list = new ArrayList<Integer>();
helper(nums,0,lists,list);
return lists;
}
private void helper(int[] nums,int level,List<List<Integer>> lists,List<Integer> list){
if(level==nums.length){
lists.add(new ArrayList<Integer>(list));
return ;
}
else{
/***********************************************************
* [[1, 2, 3], [1, 2], [1, 3], [1], [2, 3], [2], [3], []]
*/
// list.add(nums[level]);
// helper(nums,level+1,lists,list);
// list.remove(list.size()-1);
// helper(nums,level+1,lists,list);
/*************************************************
* [[], [3], [2], [2, 3], [1], [1, 3], [1, 2], [1, 2, 3]]
*/
helper(nums,level+1,lists,list);
list.add(nums[level]);
helper(nums,level+1,lists,list);
list.remove(list.size()-1);
}
}#method 4
采用回溯递归的方式,有时可以剪枝处理
首先我们需要对集合排序,对于一个n元素的集合,首先我们取第一个元素,加入子集合中,后面的n - 1个元素可以认为是第一个元素的子节点,我们依次遍历,譬如遍历到第二个元素的时候,后续的n - 2个元素又是第二个元素的子节点,再依次遍历处理,直到最后一个元素,然后回溯,继续处理。处理完第一个元素之后,我们按照同样的方式处理第二个元素。
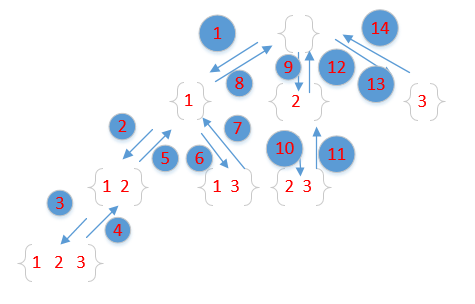 ;
;
/*********************************************************************
* 基于回溯法递归方式求子集
* 就是每当我们添加了一个元素,都是一个新的子集。那么我们怎么保证不会出现重复集合呢。
* 我们引入一个int pos用来记录此子集的起点在哪,比如当pos = 1的时候就是从第二个元素往后循环添加元素(0 base),
* 每次当此层用了第i个元素,那么下一层需要传入下一个元素的位置i+1 除此之外,
* 当循环结束要返回上一层dfs的时候我们需要把这一层刚添加元素删去。
比如输入集合为[1,2,3]应当是这么运行,
[]
[1]
[1,2]
[1,2,3] //最底层子循环到头返回删去3,上一层的子循环也到头删去2
//而此时,这一层循环刚到2,删去后还可以添加一个3
[1,3] //删除3,删除1
[2]
[2,3] //删除3,删除2
[3]
*/
public List<List<Integer>> subsetsByBackTrace(int[] nums) {
List<List<Integer>> result = new ArrayList<List<Integer>>();
if (nums == null || nums.length == 0) {
return result;
}
ArrayList<Integer> list = new ArrayList<Integer>();
Arrays.sort(nums);
backTrack(result, list, nums, 0);
return result;
}
private void backTrack(List<List<Integer>> result, ArrayList<Integer> list, int[] nums, int pos) {
result.add(new ArrayList<Integer>(list));
for (int i = pos; i < nums.length; i++) {
list.add(nums[i]);
backTrack(result, list, nums, i + 1);
list.remove(list.size() - 1);
}
}